Wolf Jung   jung@mndynamics.com

• Deutsch

• Polski

• Português

Gesamtschule Aachen-Brand, Rombachstrasse 99, 52078 Aachen, Germany.

Mandel: software for real and complex dynamics

• Draw the Mandelbrot set and Julia sets in two windows at the same time. Available methods of drawing include escape time, hyperbolic components or attracting basins, distance estimate, marking external rays or puzzle-pieces. Display Julia sets on the Riemann sphere.
• Trace equipotential lines and external rays, in the parameter plane and in the dynamic plane as well.
• Discuss the combinatorics of external angles, kneading sequences, and internal addresses. Illustrate the Spider Algorithm.
• Find centers and Misiurewicz points in the parameter plane, or periodic and preperiodic points in the dynamic plane.
• Illustrate renormalization by marking small Mandelbrot sets and small Julia sets. Mark embedded Julia sets by a kind of preperiodic renormalization.
• Display the asymptotic self-similarity at Misiurewicz points on multiple scales, and the local similarity to Julia sets.
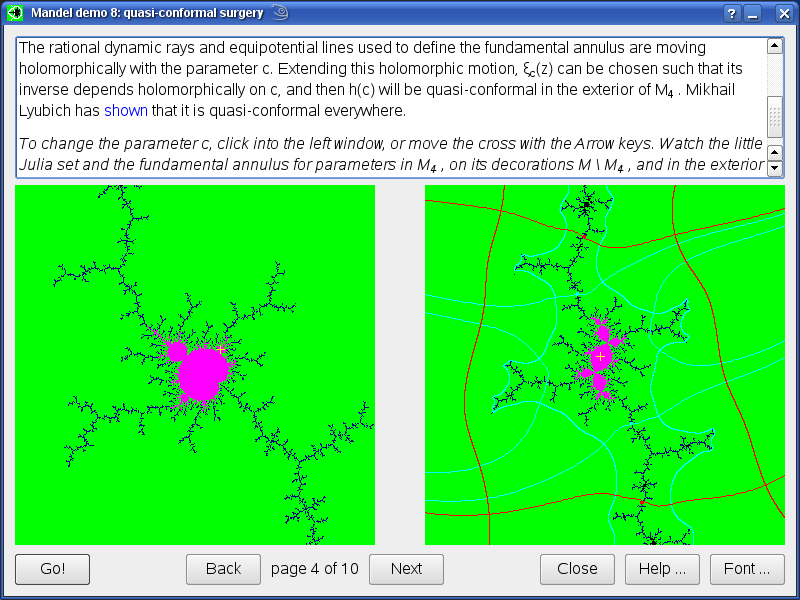
• Draw the parameter plane and Julia sets for other one-parameter families, which satisfy critical relations or show a persistent Siegel disk. Available are unicritical polynomials, Branner-Fagella polynomials, various families of cubic and quartic polynomials, quadratic rational mappings, Newton's method, transcendental functions, a simulation of quasi-conformal surgery, and Henon mappings.
• Save images as PostScript *.eps, save or load a *.png image.
• Animated demos are providing an extensive introduction to basic and advanced aspects of complex dynamics.
• Start Mandel from the GAP package FR by Laurent Bartholdi. E.g., this package can compute a mating from combinatorial data.
• Future plans include the construction of Hubbard trees and incorporating real iteration.
• The program contains a few languages: English, German, Polish (by Adam Majewski), and Portuguese (by Atractor).

Download Juliette 1.0 here, a Java applet providing external rays, renormalization, asymptotic and local similarity.

Other sites with programs on complex dynamics or fractals:
IMS, Arnaud Chéritat, Curt McMullen, Mitsuhiro Shishikura, Xaos, Fractint.

Just for fun ... a PostScript program for computing M. You may change parameters by editing the source code. Download mc.eps (1.4 kb).

The DOS-program logistic.exe deals with the real iteration of z² + c, which is conjugate to the standard logistic map. It provides features like drawing q-curves, finding hyperbolic intervals or periodic points, cobweb graphics. This program may be used and redistributed without restriction. It comes with no warranty.
Download logistic.exe 2.0 of July 30, 1998. Preliminary manual logistic.ps.

How to draw external rays:

Background:

(1)  Φ_c(z) = lim_n→∞ (f_cⁿ(z))^1/2n

for a suitable choice of the 2ⁿ-th root. This is made precise by the following formula, which is valid for large |z| with the principal value of the roots:

(2)  Φ_c(z) = z ∏_n=1^∞ (1 + c/(f_c^n-1(z))²) ^1/2n = z ∏_n=1^∞ (f_cⁿ(z)/(f_cⁿ(z)-c)) ^1/2n.

In the dynamics of quadratic polynomials, there is a basic dichotomy:

• When the critical orbit stays bounded, then the Julia set is connected, and Φ_c(z) extends to a conformal mapping from its exterior to the exterior of the unit disk. External rays and equipotential lines in the dynamic plane are defined as preimages of straight rays and circles, respectively. By definition, the parameter c belongs to the Mandelbrot set M.
• When the critical orbit escapes to ∞, the Julia set is totally disconnected, and the parameter c is not in M. Now Φ_c(z) does not extend to the critical point z = 0, e.g., but it is well-defined at the critcal value z = c.

Computation of the external argument:

(3)  arg_c(z) = arg(z) + ∑_n=1^∞ 1/2ⁿ arg(1 + c/(f_c^n-1(z))²) = arg(z) + ∑_n=1^∞1/2ⁿ arg(f_cⁿ(z)/(f_cⁿ(z)-c)).

Here arg(z) denotes the argument of the complex number z, i.e., its angle to the positive real axis. This angle is defined only up to multiples of 2π. E.g., a point z on the negative real axis has the arguments ±π, ±3π, ±5π ... The principal value of the argument is the unique angle with -π<arg(z)≤π. This definition is used because a function should be single-valued. However, a discontinuity is introduced artificially when a point z is crossing the negative real axis, say going from i to -1 to -i: its argument should go from π/2 to π to 3π/2, but the principal value goes from π/2 to π, jumps to -π, and goes to -π/2.

Formula (3) means that the orbit z_n=f_cⁿ(z) of z and the arguments arg(z_n/(z_n-c)) are computed. The function arg(z/(z-c)) is discontinuous on the straight line segment from the critical point z = 0 to the critical value z = c, which is drawn in red in the figure: when z belongs to this line segment, then z/(z-c) will be on the negative real axis. When the Julia set is connected, the location of the discontinuity can be moved onto a kind of curve joining 0 and c within the Julia set, such that the argument is continuous in the whole exterior:

• Suppose that z is crossing the red line from right to left, and moving to the fixed point α_c and beyond. The principal value arg(z/(z-c)) is jumping from π to -π at the red line, goes up to about -0.68π at α_c and stays continuous there.
• The modified function arg(z/(z-c)) is continuous with value π, as z is crossing the red line. It goes up to about 1.32π when z is approaching α_c from the right, and jumps to about -0.68π as z is crossing α_c to the left.

The same modification seems to work for the computation of the argument arg_M(c) in the parameter plane as well, although the Julia set is disconnected. The left image below shows the discontinuities arising from the principal value of arg(z/(z-c)) in (3), they are appearing on curves joining centers of different periods. In the right image, the argument is adjusted, and the discontinuities are moved closer to the Mandelbrot set.

Drawing “all” rays:

Drawing a single ray:

• In the dynamic plane, external rays can be drawn by backwards iteration: It is most effective for a periodic or preperiodic angle. You must keep track of points on the finite collection of rays with angles θ, 2θ, 4θ ... Say z_l,j corresponds to a radius R^1/2l and the angle 2^jθ. Then f_c(z) maps z_l,j to z_(l-1),(j+1). This point, which was constructed before, has two preimages under f_c(z) . The one that is closer to z_(l-1),j is the correct one. This criterion was proved by Thierry Bousch. The ray will look better when you introduce intermediate points. Backwards iteration is used in Mandel again since version 5.3, both in the plane and on the sphere. The current implementation consists of QmnPlane::backRay().

• Choose a sequence of radii tending to 1, e.g., R_n = R^1/2n with R large. Search corresponding points on the ray, which satisfy Φ_c(z_n) = R_n e^iθ or Φ_M(c_n) = R_n e^iθ, respectively. To this end, the Newton method is employed. Using the approximation (1), the function N(z) = z - P(z)/P'(z) is iterated to find a zero of P(z) = f_cⁿ(z) - R e^i2nθ, or analogously in the parameter plane. Intermediate points should be used to make the curve between the points smooth, and to reduce the danger of the Newton method failing when the previous point is not in the immediate basin of attraction for the new point. Presumably, this method has been developed by John Hamal Hubbard or John Milnor, and it has been implemented by Arnaud Chéritat, Christian Henriksen and Mitsuhiro Shishikura as well. It is used in Mandel since version 5.4, the current implementation consists of QmnPlane::newtonRay() and QmnPlane::rayNewton(). These were ported to Java as well. The paper by Tomoki Kawahira gives a detailed description and an error estimate for the approximation (1).
• There are two approaches to draw the external ray of angle θ by computing the external argument (3): Argument scanning means to check every pixel, which is very slow, but might be improved by a recursive subdivision of the image. Argument tracing means to construct a sequence of triangles along the ray. (I have learned this technique from Chapter 14 in this book, where boundary tracing is used to draw escape lines.) First two pixels at the border of the image are found, such that the external argument is <θ at P₀ and ≥θ at P₁. Then compute the external argument at the third vertex P₂:
  • If it is <θ, then the ray is intersecting the edge from P₁ to P₂. Reflect the triangle along this edge to obtain the new vertex P₂, rename the old vertex P₂ to P₀, and keep P₁.
  • If it is ≥θ, then the ray is intersecting the edge from P₀ to P₂. Reflect the triangle along this edge to obtain the new vertex P₂, rename the old vertex P₂ to P₁, and keep P₀.
  Repeat this process with the new triangle … and draw the ray along the sequence of triangles. This basic idea can be improved in several ways:
  • To make the ray look smooth, draw line segments instead of single pixels. Choose the way of reflection such that the distance to previously drawn pixels is increased.
  • Check this distance also to avoid going in circles around the endpoint. (This is not yet implemented in the current version of Mandel.)
  • When computing the external argument according to (3), adjust the principal value of arg(z_n/(z_n-c)) by ±2π, if z_n=f_cⁿ(z) or z_n=f_cⁿ(c) is in the triangle between 0, c, and α_c as explained above.
  • Save the intermediate arguments arg(z_n/(z_n-c)) for the next pixel to check for jump discontinuities by comparison, and to adjust them. (The previous technique shifts these closer to the boundary, but does not remove them.) A drawback of this approach is that it restricts the number of iterations to the length of the array, which means in particular that the end of the ray may be lost.
  • When the image shows a very small part of the Julia set or Mandelbrot set, maybe the starting point will not be found in spite of the previous techniques. It can be searched for on the boundary of a virtual enlarged image, but this will be impractical when it is necessary to enlarge the image by several orders of magnitude.
  Argument tracing has been used in Mandel since 1997, the current implementation consists of mndlbrot::turnsign() and QmnPlane::traceRay().
• Johannes Riedl has used a method, where the next point is chosen from a finite collection of points at a prescribed distance from the last one.
• The power series expansion of Φ_c^-1 or Φ_M^-1 could be used as well to draw external rays, but I expect it to converge extremely slowly close to the boundary.
• Noting that the direction of an external ray is determined uniquely from the fact that it is orthogonal to the equipotential line, external rays can be drawn by solving a differential equation numerically. I am not sure if this method will be numerically stable, and I have received different claims about it.

Note that most of the methods above can be modified to draw equipotential lines. In this case there is no problem with the ambiguity of the argument. Boundary scanning is slow and the Newton method has three problems: finding a starting point, drawing several lines around a disconnected Julia set, and choosing the number of points depending on the chosen subset of the plane. Therefore I am using boundary tracing with starting points on several lines through the image. See QmnPlane::green(). Still, sometimes not the whole line is drawn, or not all components are found.